|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
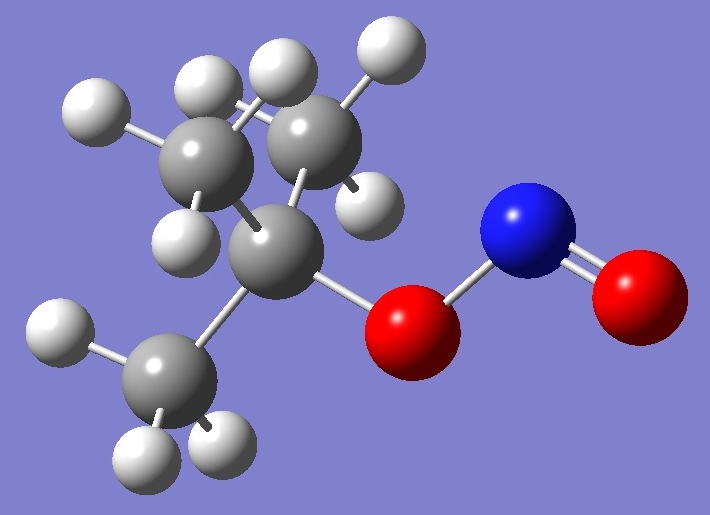
(CH3)3CO-N=O
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nitrogen
|
|
|
Nuclear
Quadrupole Coupling Constants |
|
|
|
in tert-Butyl Nitrite |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14N nqcc's in, and a heavy atom substitution structure of tert-butyl nitrite were determined by Heineking et al. [1]. |
|
|
|
|
|
|
|
|
|
|
|
|
Calculation of the nqcc's was made here on the substitution structure. These are
compared with the experimental nqcc's in Table 1.
Structure parameters are given in Table 2. |
|
|
|
|
|
|
|
|
|
|
|
|
In Table 1, subscripts a,b,c refer to the principal axes of the inertia
tensor, subscripts x,y,z to the principal axes of the nqcc tensor.
The nqcc y-axis is chosen coincident with the inertia c-axis, these
are perpendicular to the Cs plane of the molecule. Ø (degrees)
is the angle between its subscripted parameters. ETA = (Xxx
- Xyy)/Xzz. |
|
|
RMS is the root mean square
difference between calculated and experimental nqcc's (percentage of
average experimental nqcc). RSD is the residual standard deviation
of calibration of the B3PW91/6-311+G(df,pd) model for calculation of
the nqcc's. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
Table 1.
Nitrogen nqcc's in tert-Butyl Nitrite (MHz). |
|
| |
|
|
|
|
|
|
|
|
|
|
|
Calc. |
|
Expt. [1] |
|
| |
|
|
|
|
|
|
|
|
14N |
Xaa |
|
0.779 |
|
0.8536(10) |
|
|
|
Xbb |
- |
4.380 |
- |
4.2307 |
|
|
|
Xcc |
|
3.601 |
|
3.3771(11) |
|
|
|
|Xab| |
|
3.149 |
|
|
|
|
|
|
|
|
|
|
|
|
|
RMS |
|
0.161 (5.7 %) |
|
|
|
|
|
RSD |
|
0.030 (1.3 %) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Xxx |
|
2.270 |
|
2.15(17) |
|
|
|
Xyy |
|
3.601 |
|
3.377(1) |
|
|
|
Xzz |
- |
5.871 |
- |
5.53(17) |
|
|
|
ETA |
|
0.227 |
|
|
|
|
|
Øx,a |
|
25.34 |
|
24.3(13) |
|
|
|
Øz,bi * |
|
17.60 |
|
16.5(13) |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
* Angle between the bisector ('bi') of the ONO angle and the z-principal axis of the nqcc tensor. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculation of the nqcc
tensor was made on the heavy atom substitution structure, with the
hydrogens located by partial optimization (fixed heavy atom structure)
at the MP2/6-31G(d,p) level of theory. The CH bond lengths were
corrected using r = 1.001 ropt,
where ropt are the MP2/6-31G(d,p) bond lengths [3]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Table 2. tert-Butyl Nitrite. Heavy atom molecular structure parameters (Å
and degrees). Complete structure is given here in Z-matrix format. |
| |
|
|
|
|

|
O(1)=N |
1.18183(79) |
|
N-O(3) |
1.41751(78) |
|
O(3)C(4) |
1.43752(62) |
|
C(4)C(5) |
1.52341(28) |
|
C(4)C(6,7) |
1.52902(44) |
|
ONO |
111.59(20) |
|
NOC |
111.76 |
|
|
OCC(5) |
103.03(10) |
|
|
OCC((6,7) |
110.09(8) |
|
|
NOCC(6,7) |
61.55(10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[1] N.Heineking, W.Jäger, and M.C.L.Gerry, J.Mol.Spectrosc. 155,403(1992).
|
|
|
[2] J.Demaison and G.Wlodarczak, Structural
Chem. 5,57(1994). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table of Contents |
|
|
|
|
|
Molecules/Nitrogen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CH33CONO.html |
|
|
|
|
|
|
Last
Modified 13 April 2008 |
|
|
|
|
|
|
|
|
|
|

