|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CF3N=C=O
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nitrogen |
|
|
|
Nuclear
Quadrupole Coupling Constants |
|
|
|
in Trifluoromethyl Isocyanate |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculation was made of the 14N nqcc tensor in trifluoromethyl isocyanate on ropt structures given by B3LYP/6-311+G(3df,3pd) and MP2/6-311+G(3df,3pd) optimization.
|
|
|
|
|
|
|
|
|
|
|
|
|
In Table 1, these calculated nqcc's are compared with the experimental values of Koput et al. [1]. Subscripts
a,b,c refer to the principal axes of the inertia tensor.
Subscripts x,y,z refer to the principal axes of the nqcc tensor. ETA = (Xxx - Xyy)/Xzz. Ø
(degrees) is the angle between its subscripted parameters.
RMS is the root mean square difference between calculated and
experimental nqcc's (percentage of average experimental nqcc).
RSD is the residual standard deviation of calibration of the B3PW91/6-311+G(df,pd) model for calculation of the efg's/nqcc's.
|
|
|
Structure parameters are given in Z-matrix format in Table 2, rotational constants are given in Table 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Table 1. 14N nqcc's in CF3N=C=O (MHz). Calculation was made on ropt molecular structures given by B3LYP/6-311+G(3df,3pd) and MP2/6-311+G(3df,3pd) optimization. NOTE: Calculated Xbb and Xcc have been reversed (see below).
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
Calc. B3LYP
|
|
Calc. MP2
|
|
Expt. [1] |
|
| |
|
|
|
|
|
|
|
|
|
Xaa |
|
3.309 |
|
3.249 |
|
3.2977(8)
|
|
|
Xbb |
- |
2.079 |
- |
2.118 |
-
|
2.1313(40)
|
|
|
Xcc |
- |
1.230 |
- |
1.132
|
-
|
1.1664(40)
|
|
|
|Xac| |
|
0.258 |
|
0.209 |
|
0.227(19)
|
|
|
|
|
|
|
|
|
|
|
|
RMS
|
|
0.048 (2.2 %)
|
|
0.035 (1.6 %)
|
|
|
|
|
RSD |
|
0.030 (1.3 %) |
|
0.030 (1.3 %) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Xxx |
- |
2.079
|
- |
2.118
|
-
|
2.1313
|
|
|
Xyy |
- |
1.245
|
- |
1.142 |
-
|
1.1779
|
|
|
Xzz |
|
3.324 |
|
3.259 |
|
3.3092
|
|
|
ETA |
|
0.251 |
|
0.299 |
|
|
|
|
Øz,a |
|
3.25 |
|
2.73
|
|
2.90
|
|
|
Øa,N=C |
|
|
|
|
|
|
|
|
Øz,N=C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Table 2. CF3N=C=O. Structure parameters, B3LYP/6-311+G(3df,3pd) and MP2/6-311+G(3df,3pd) (Å
and degrees).
|
| |
|
|
|
|
|
|
|
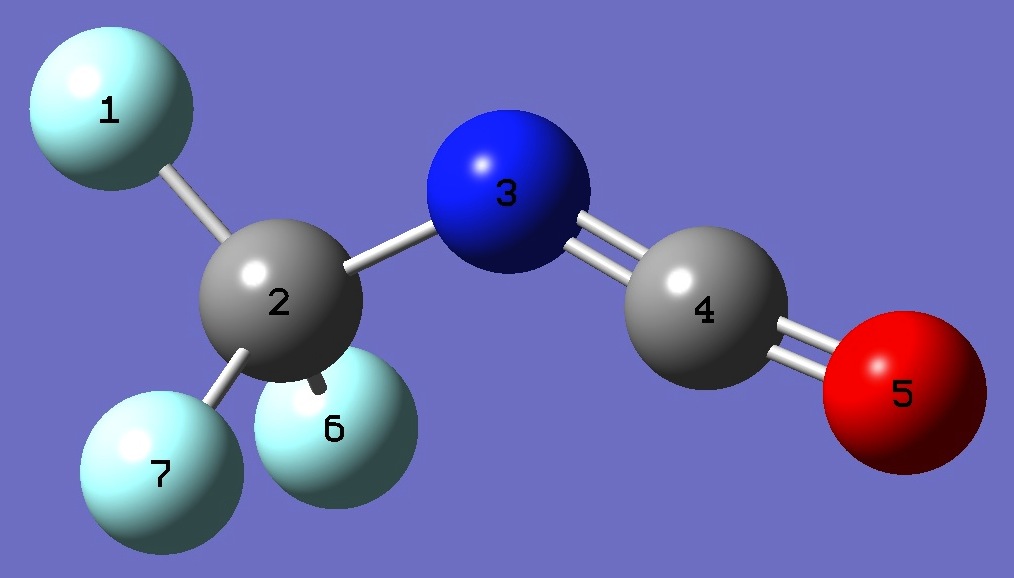
|
F
C,1,B1
N,2,B2,1,A1
C,3,B3,2,A2,1,D1,0
O,4,B4,3,A3,2,D2,0
F,2,B5,3,A4,4,D3,0
F,2,B6,3,A5,4,D4,0
|
|
|
|
|
|
|
|
|
|
|
|
B3LYP
|
MP2 |
|
|
B1=1.33036372
B2=1.40287148
B3=1.21304848
B4=1.15563981
B5=1.34339482
B6=1.34339482
A1=109.56903999
A2=130.97237598
A3=173.3896775
A4=111.94970035
A5=111.94970035
D1=180.
D2=180.
D3=-60.23444432
D4=60.23444432
|
B1=1.32292923
B2=1.40462186
B3=1.22216511
B4=1.16338695
B5=1.33485641
B6=1.33485641
A1=109.21817901
A2=127.75175369
A3=172.70146532
A4=111.76568662
A5=111.76568662
D1=180.
D2=180.
D3=-60.27908605
D4=60.27908605
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NOTE:
As can be seen in Table 1, good agreement between calculated and
experimental inertial axes nqcc's is obtained if calculated Xbb and Xcc
are reversed. As can be seen in Table 3, there is little
difference between B and C rotational constants. Calculated
rotational constants are rigid molecule values, whereas the
experimental values are measured in the ground vibrational state of the
molecule. So, I assume that consideration of zero point
vibrational effects could easily reverse the nearly equal Be and Ce, and thus Xbb and Xcc. Alternatively, small changes in some optimized structural parameters could accomplish this same reversal.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 3. CF3N=C=O. Rotational Constants (MHz).
|
|
|
|
|
|
|
|
|
B3LYP
|
MP2
|
|
Expt [1]
|
|
|
|
|
|
|
|
Ae
|
5637
|
5685
|
Ao |
5675 (fixed)
|
|
Be
|
1719
|
1744
|
Bo |
1752.5237(20)
|
|
Ce
|
1715
|
1739
|
Co |
1746.1322(20)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[1] J.Koput, W.Stahl, N.Heineking, G.Pawelke, B.Steger, and D.Christen, J.Mol.Spectrosc. 168,323(1994). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HNCO
|
CH2C(H)NCO
|
(CH3)3CNCO
|
CH3CH2NCO
|
|
|
CH3NCO
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table of Contents |
|
|
|
|
|
Molecules/Nitrogen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CF3NCO.html |
|
|
|
|
|
|
Last
Modified 27 March 2015
|
|
|
|
|
|
|
|
|
|
|

